I recently had some time to think about the following cryptography problem:
I've written up a short example in Python3 to show this in action (in case you doubt me!)
For more information: Davies-Meyer.
Given two functions, 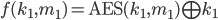 and
and 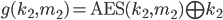 find
corresponding
find
corresponding 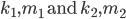 such that a collision between the functions occurs.
Logically this means you need to find the correct arguments such that
such that a collision between the functions occurs.
Logically this means you need to find the correct arguments such that 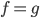 .
.
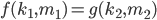
apply definitions of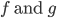
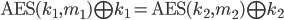
xor both sides by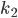

apply AES decryption to both sides with key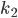
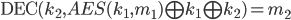
Now we have solved for message 2; the other values we can simply choose at random.
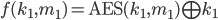 and
and 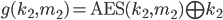 find
corresponding
find
corresponding 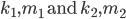 such that a collision between the functions occurs.
Logically this means you need to find the correct arguments such that
such that a collision between the functions occurs.
Logically this means you need to find the correct arguments such that 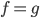 .
.
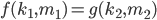
apply definitions of
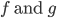
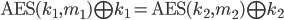
xor both sides by
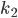

apply AES decryption to both sides with key
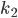
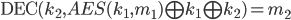
Now we have solved for message 2; the other values we can simply choose at random.
I've written up a short example in Python3 to show this in action (in case you doubt me!)
from Crypto.Cipher import AES
from Crypto.Util.strxor import strxor as xor
from Crypto import Random
from binascii import hexlify as hexify
# find a, b, x, and y such that
# AES(y, x) XOR y == AES(b, a) XOR b
# Note that for clarity, these names are not used
# each variable is referred to as a m (message) or a k(key)
# and AES takes arguments (key, message)
def collision():
random = Random.new()
k1 = random.read(16)
m1 = random.read(16)
k2 = random.read(16)
key1 = AES.new(k1, AES.MODE_ECB)
key2 = AES.new(k2, AES.MODE_ECB)
m2 = key2.decrypt(xor(xor(key1.encrypt(m1), k1), k2))
xor1 = xor(key1.encrypt(m1), k1)
xor2 = xor(key2.encrypt(m2), k2)
print("key 1: %s\nkey 2: %s" %(hexify(k1), hexify(k2)))
print("msg 1: %s\nmsg 2: %s" %(hexify(m1), hexify(m2)))
print("AES(key1, msg1) xor key1: %s\nAES(key2, msg2) xor key2: %s" %(hexify(xor1), hexify(xor2)))
if __name__ == '__main__':
collision()
For more information: Davies-Meyer.
Cryptography
Python